こんにちは、電太です。
2022年6月24日に始まった、Steamのサマーセールも半分経過しました。
一般的にセールの割引率は時間の経過とともに上がっていくため、次回のセールではさらに安くなる可能性があります。
そのため、すぐにやる予定のないゲーム(=積みゲー)を今買うべきかどうか、迷う方も多いのではないでしょうか。
そこで、買い時を以下の2点で定義し、今回のSteamサマーセールでお目当てのゲームを購入するどうかをジャッジするというのが記事の目的です。
- 平均的な割引率よりも大きい割引率が設定されているゲーム
=何らかの理由により大幅な割引を実施しているゲーム - 今回のセールと次回のセールで割引率が変わらなそうなゲーム
=半年先のセールを待っても安くならないゲーム
上で定義した平均的な割引率と次回のセールの割引率を知るためには、まず、割引率の予測モデルを作成する必要があります。
本記事ではこのモデルの作成を中心に説明します。
さらに、今後の記事で、上で定義した2つの買い時を取り上げる予定です。
※割引率の予測はあくまで過去の実績に基づいた期待値で、当たることもあれば外れることもあります。
当ブログは掲載内容によって生じた損害に対する一切の責任を負いません。
こんな人向けの記事です。
- 今回のSteamサマーセールでお目当てのゲームを購入するか、次のセールまで待つか、迷っている人
広告
概要
記事の流れ
上に述べた平均的な割引率と次回のセールの割引率を知るためには、まず、割引率の予測モデルを作成する必要があります。
さらに、割引率が大きく上がる期間を予測し、購入を待ったほうが良い期間をゲームタイトルの価格帯別に明らかにします。
ここで、本記事の大まかな流れを以下に示します。
- モデル作成に必要なデータを集めます
- データに基づいた予測モデルを作成します
- 予測モデルを使って、購入の先延ばしを検討したほうが良い期間を明らかにします
調査
2022年7月2日時点でGoogle先生に「steam 割引率 予測 予想」や「steam 価格 予測 予想」を聞いてもヒットするものがなかったため、独自の方法で予測モデルを作成しています。
また、先行研究として「Steam Game Discount Prediction Using Machine Learning Methods」が発表されていますが、課金が必要なため、著者はこの論文の内容を確認していません。
割引率の予測モデル作成に必要なデータ
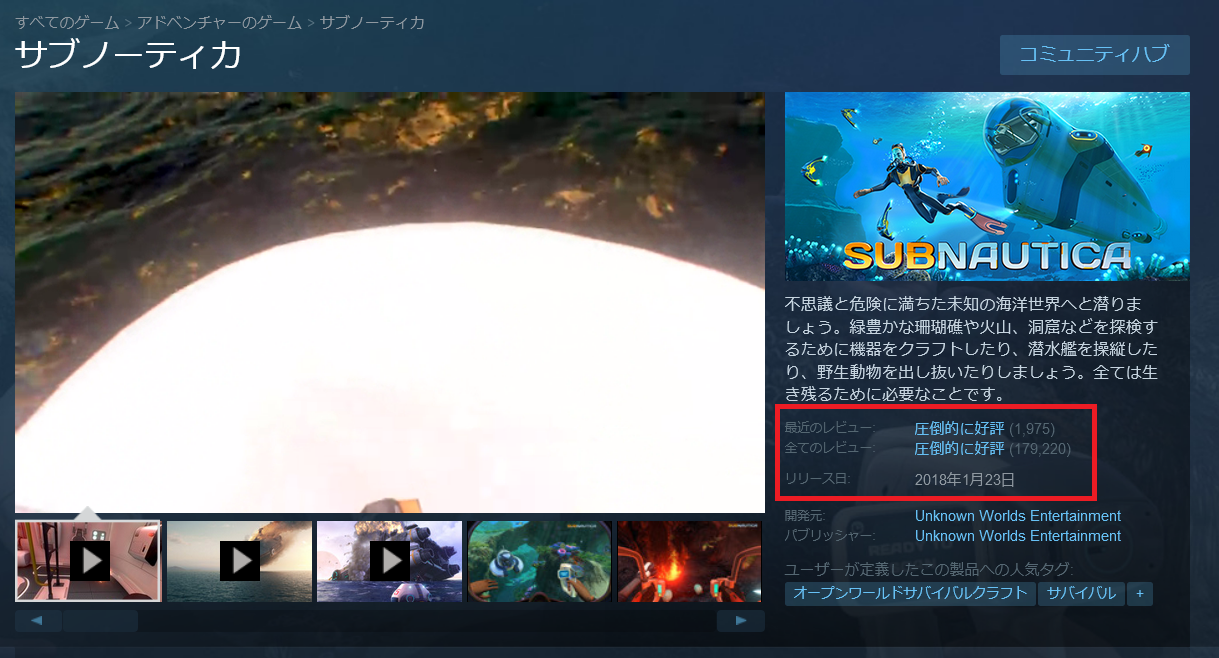
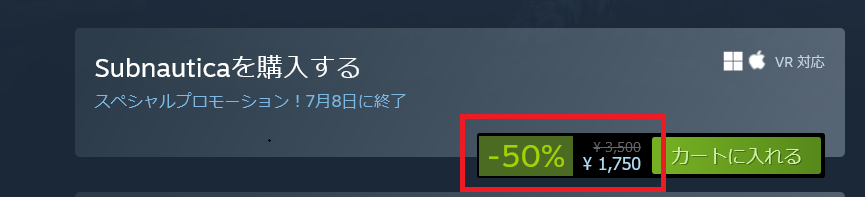
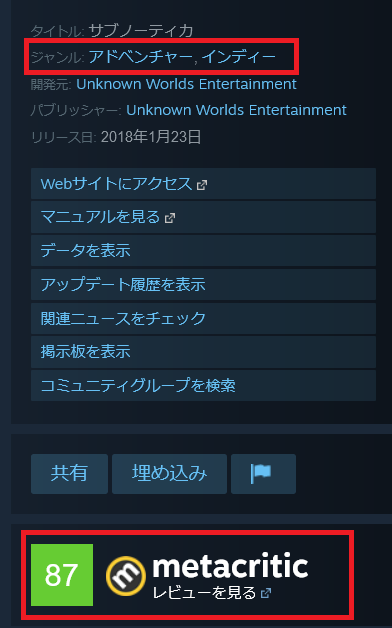
必要なデータはSteamで割引が設定されている1294タイトルを対象とし、各タイトルについて以下の項目をピックアップしました。
- 割引率
- リリース時の価格 $
- リリース日
- ジャンル
- メタスコア
- 最近のレビュー
- レビュー数
- 高評価の割合
- すべてのレビュー
- レビュー数
- 高評価の割合
なお、それぞれの項目は次の位置に掲載されています。
https://store.steampowered.com/app/264710/_/参照
また、ピックアップしたタイトルの一部に以下のようなゲームタイトルが含まれています。
- Tom Clancy’s Rainbow Six Siege
- Terraria
- Garry’s Mod
- Rust
- The Witcher 3: Wild Hunt
- Among Us
- Dead by Daylight
- Cyberpunk 2077
- Stardew Valley
- Euro Truck Simulator 2
割引率の予測モデル
データについて
データは学習用のデータとテスト用のデータに分割しています。
また、特徴量について、リリース日はリリースからの経過日としています。
そのほか、レビュー数と経過日から一日あたりのレビュー数を算出したり、レビュー数と高評価の割合と経過日から1日あたりの高評価数を特徴量に追加しています。
ゲームの割引率予測モデル
ゲームの割引率予測モデルはPythonのパッケージであるPyCaretを使って作成します。
compare_models
まずは、compare_modelsでモデルの精度比較を行い、結果を下の表に示します。
gbrのR2が最も高い0.449で、ランダムフォレストのR2は二番目に高い0.4437であることが分かります。
RMSEは13程度なので、予測誤差は小さくありませんでした。
| Model | MAE | MSE | RMSE | R2 | RMSLE | MAPE | TT (Sec) | |
|---|---|---|---|---|---|---|---|---|
| gbr | Gradient Boosting Regressor | 10.5972 | 177.3537 | 13.2179 | 0.449 | 0.267 | 0.2265 | 0.042 |
| rf | Random Forest Regressor | 10.6078 | 179.227 | 13.2795 | 0.4437 | 0.2682 | 0.2264 | 0.106 |
| br | Bayesian Ridge | 10.887 | 179.9921 | 13.3697 | 0.4367 | 0.2694 | 0.2315 | 0.006 |
| ridge | Ridge Regression | 10.8855 | 180.5985 | 13.3904 | 0.4351 | 0.2709 | 0.2312 | 0.007 |
| lr | Linear Regression | 10.8894 | 180.917 | 13.4015 | 0.4341 | 0.2716 | 0.2312 | 0.753 |
| lar | Least Angle Regression | 10.8894 | 180.9169 | 13.4015 | 0.4341 | 0.2716 | 0.2312 | 0.008 |
| huber | Huber Regressor | 10.8749 | 182.7915 | 13.4684 | 0.4284 | 0.2761 | 0.2335 | 0.019 |
| ada | AdaBoost Regressor | 11.3123 | 188.687 | 13.6918 | 0.409 | 0.2728 | 0.2363 | 0.03 |
| et | Extra Trees Regressor | 10.972 | 190.9149 | 13.7172 | 0.4059 | 0.275 | 0.2334 | 0.095 |
| lightgbm | Light Gradient Boosting Machine | 11.0083 | 194.9057 | 13.8379 | 0.3936 | 0.2741 | 0.2322 | 0.026 |
| lasso | Lasso Regression | 11.618 | 202.5256 | 14.1794 | 0.3665 | 0.2918 | 0.2583 | 0.007 |
| en | Elastic Net | 12.1653 | 217.4485 | 14.702 | 0.3206 | 0.3055 | 0.2745 | 0.008 |
| omp | Orthogonal Matching Pursuit | 12.0119 | 218.821 | 14.742 | 0.3154 | 0.3 | 0.2664 | 0.007 |
| knn | K Neighbors Regressor | 11.8428 | 222.4877 | 14.8118 | 0.3087 | 0.3039 | 0.2668 | 0.008 |
| par | Passive Aggressive Regressor | 13.051 | 266.9204 | 16.2074 | 0.1649 | 0.3274 | 0.2813 | 0.008 |
| llar | Lasso Least Angle Regression | 15.15 | 322.3569 | 17.9197 | -0.0085 | 0.3627 | 0.3452 | 0.007 |
| dummy | Dummy Regressor | 15.15 | 322.357 | 17.9197 | -0.0085 | 0.3627 | 0.3452 | 0.007 |
| dt | Decision Tree Regressor | 14.077 | 336.1079 | 18.2628 | -0.0674 | 0.3597 | 0.2863 | 0.006 |
create_model
ここではinterpret_modelの使えるランダムフォレストを使います。
次に示す各foldの精度一覧より、R2は0.2902から0.6346で、foldごとのばらつきが大きいことが分かります。
| Fold | MAE | MSE | RMSE | R2 | RMSLE | MAPE |
|---|---|---|---|---|---|---|
| 0 | 12.6627 | 242.5903 | 15.5753 | 0.2902 | 0.3263 | 0.291 |
| 1 | 12.23 | 239.1329 | 15.4639 | 0.298 | 0.324 | 0.289 |
| 2 | 11.9434 | 210.9958 | 14.5257 | 0.4374 | 0.2736 | 0.2346 |
| 3 | 11.1969 | 182.5649 | 13.5117 | 0.4214 | 0.2704 | 0.2373 |
| 4 | 9.6431 | 155.4215 | 12.4668 | 0.5028 | 0.2426 | 0.1955 |
| 5 | 10.5593 | 197.0926 | 14.039 | 0.4372 | 0.2972 | 0.2439 |
| 6 | 10.1733 | 150.7532 | 12.2782 | 0.531 | 0.2493 | 0.1998 |
| 7 | 8.4731 | 116.3269 | 10.7855 | 0.6346 | 0.2533 | 0.2082 |
| 8 | 10.8036 | 189.7977 | 13.7767 | 0.3749 | 0.2623 | 0.2131 |
| 9 | 8.393 | 107.594 | 10.3728 | 0.5097 | 0.1828 | 0.1514 |
| Mean | 10.6078 | 179.227 | 13.2795 | 0.4437 | 0.2682 | 0.2264 |
| Std | 1.4003 | 44.1816 | 1.6972 | 0.101 | 0.0399 | 0.0405 |
tune_model
ここではモデルパラメータの最適化を行い、結果を下の表に示します。
R2は0.3391から0.655と精度のばらつきは大きいものの、パラメータの最適化による精度の向上が確認できました。
| Fold | MAE | MSE | RMSE | R2 | RMSLE | MAPE |
|---|---|---|---|---|---|---|
| 0 | 12.2424 | 225.8786 | 15.0293 | 0.3391 | 0.3132 | 0.2791 |
| 1 | 11.8283 | 223.7189 | 14.9572 | 0.3433 | 0.3178 | 0.2835 |
| 2 | 11.8362 | 206.7733 | 14.3796 | 0.4486 | 0.2729 | 0.2356 |
| 3 | 11.1747 | 174.4737 | 13.2088 | 0.4471 | 0.2634 | 0.2351 |
| 4 | 9.8214 | 153.7534 | 12.3997 | 0.5081 | 0.2393 | 0.1978 |
| 5 | 10.7216 | 194.4843 | 13.9458 | 0.4447 | 0.2929 | 0.2482 |
| 6 | 10.0757 | 145.3322 | 12.0554 | 0.5479 | 0.2463 | 0.2039 |
| 7 | 8.3544 | 109.8202 | 10.4795 | 0.655 | 0.2442 | 0.2007 |
| 8 | 10.5449 | 171.6223 | 13.1005 | 0.4348 | 0.2435 | 0.207 |
| 9 | 8.6056 | 113.7416 | 10.665 | 0.4817 | 0.1905 | 0.1571 |
| Mean | 10.5205 | 171.9598 | 13.0221 | 0.465 | 0.2624 | 0.2248 |
| Std | 1.2618 | 39.5009 | 1.5444 | 0.0881 | 0.0365 | 0.0372 |
plot_model
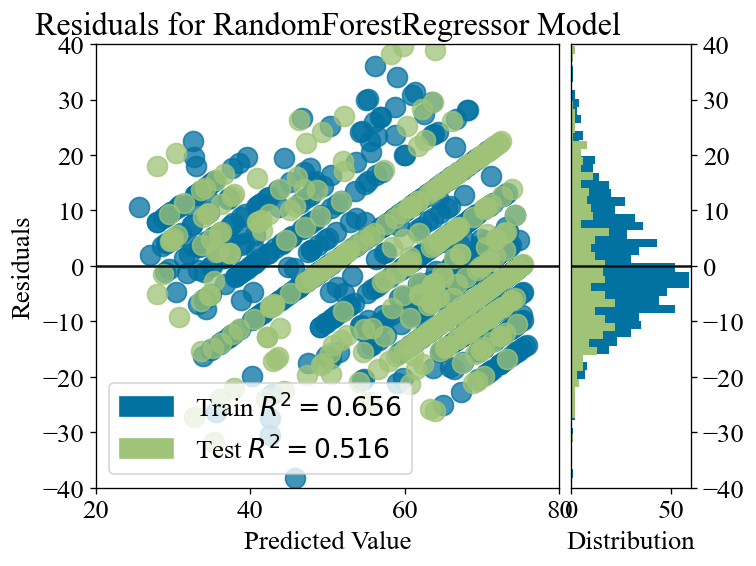
作成したモデルの予測誤差を確認します。
学習用データセットのR2が0.656に対して、検証用のデータセットのR2が0.516となり、精度はまずまずの結果でした。
特徴量と割引率の関係について
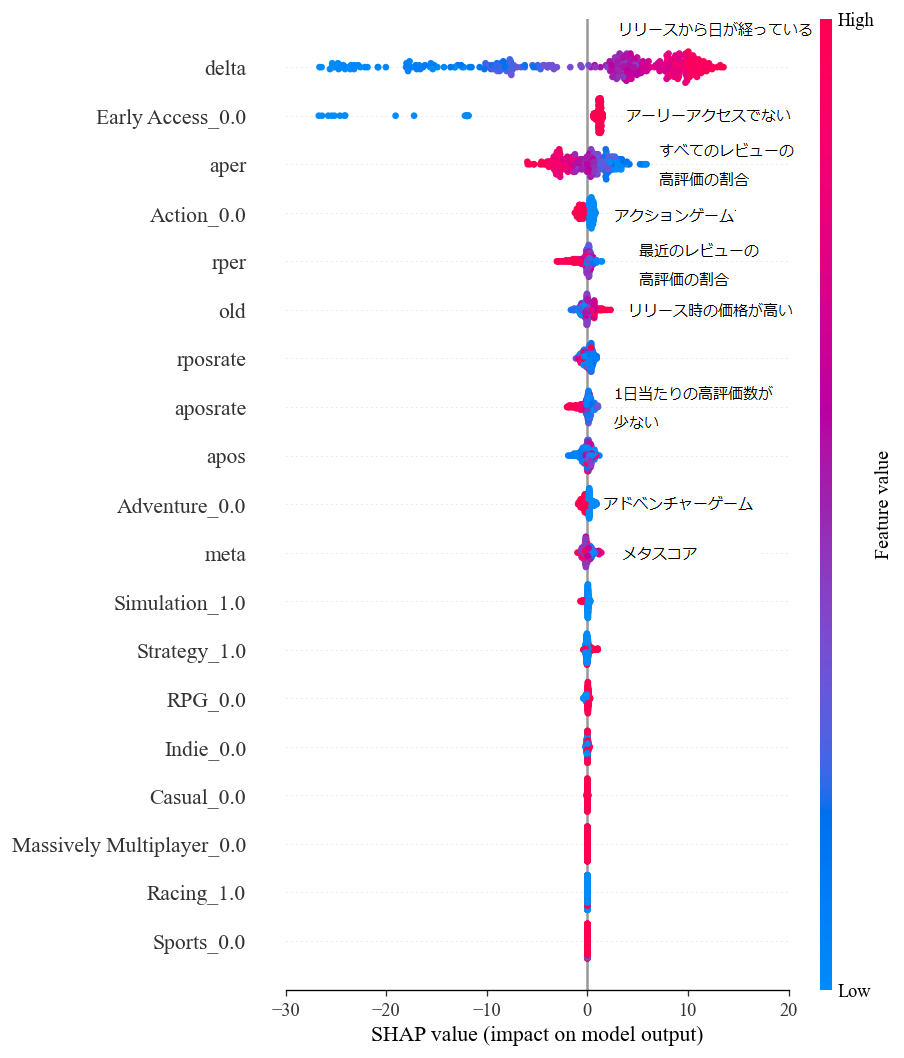
特徴量と割引率の関係について、interpret_modelでSHAP値をグラフ化したものを以下に示します。
このグラフより、どの特徴量が割引率に影響を与えているのかがわかります。
まず、リリースからの経過日の影響が最も大きく、日が経つほど割引率が高くなる傾向にあります。
これは時間が経つほど安くなるという我々の感覚と同じ結果になります。
次にアーリーアクセスでない(通常のリリース)は割引率が高い傾向となっていますが、アーリーアクセスのゲーム数が多くないので、あまり重要ではないと考えられます。
高評価の割合では、評価が低いほど割引率が高い結果になっています。
これは需要のないものは価格が下がるという市場原理が割引率に反映されていると考えられます。
ジャンルについて、アクションゲームとアドベンチャーゲームは割引率が高いことが分かります。
対して、シミュレーションゲームは割引率が低く、長く遊べるゲームの割引率は低くなる傾向が伺えます。
価格面ではリリース時の価格が高いほど割引率が高いという結果になりました。
これは元値が高いほど割引率を高く設定できるためと考えられます。
最後に、メタスコアは割引率とあまり関係がありませんでした。
以上のことをまとめると、
- ゲームのリリースから日が経つほど、またレビューの評価が低いほど、割引率は高くなります
- 価格が高いほど割引率は上がります
- ジャンルについて、アクションやアドベンチャーは割引率が高く、シミュレーションゲームは割引率が低い傾向にあります
割引率が大きく上がる期間
割引率が大きく上がる直前の期間は、できるだけゲームの購入を先延ばしにした方が良いと考えられます。
そのため、リリースからの経過日数と割引率の関係を価格帯別に計算し、購入の先延ばしを検討すべき期間を明らかにします。
まず、リリース時の価格より、20ドル以下の小型タイトル、20ドルから40ドルの中型タイトル、40ドルより大きい大型タイトルの3つに分けます。
次にそれぞれの規模のタイトルについて、特徴量の平均を計算します。
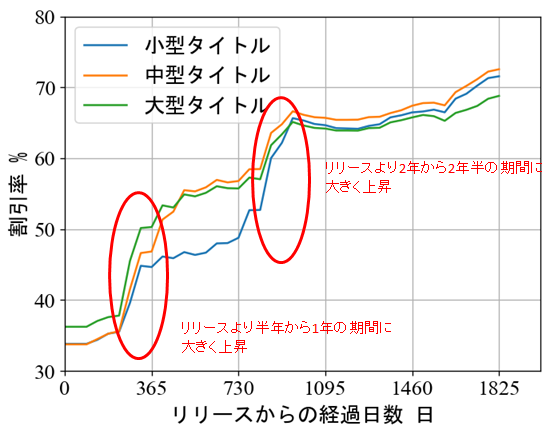
最後に特徴量の平均とモデルを使い、リリースからの経過日数と割引率の関係を可視化し、下に示します。
リリースから半年の間、割引率は35%程度となり、大型タイトルは少し高めの割引率になります。
1年後(365日後)では、大型タイトルは概ね50%の割引が期待されます。
その一方で、20ドル以下の小型タイトルの割引率は45%程度で、大型タイトルの割引率との間に差が広がり始めます。
2年後(730日後)では、中型・大型タイトルの割引率の期待値はおおよそ55%となります。
一方、小型タイトルの割引率は5%ほど低い数字になっています。
最後に2年半後(900日後)の割引率を見てみましょう。
この時点の割引率はタイトルの大きさに関係なく概ね65%となっていて、さらに、4年後まで割引率はほぼ横ばいとなります。
以上の結果より、割引率が大きく上がる直前で、購入を再検討した方が良いと考えられる期間は以下の2つの期間になります。
- リリースより半年から1年の期間
- リリースより2年から2年半の期間
まとめと今後
本記事を以下にまとめます。
- ゲームの割引率予測モデルを作成しました
- 割引率はゲームリリースからの日数やレビューの評価などの影響を受けていることを明らかにしました
- リリースより半年ないし2年経ったゲームは、その後のセールでさらに安くなる可能性が高いため、購入の先延ばしを検討した方が良いことがわかりました
今後の記事では、以下の2点で定義する買い時のゲームをリストアップする予定です。
- 平均的な割引率よりも大きい割引率が設定されているゲーム
=何らかの理由により大幅な割引を実施しているゲーム - 今回のセールと次回のセールで割引率が変わらなそうなゲーム
=半年先のセールを待っても安くならないゲーム
広告
広告